Mit gondoltok, mi az összefüggés a Kvantumfizika, karfiol, páfrányok, káoszelmélet, mesterséges intelligencia és a Minecraft között?
A RoboKaland módszer egyik alappillére, hogy a bonyolultnak - tűnő - feladatokat, egyszerűbb, elemibb, könnyen érthető, "siker-élmény-orientált" és játékos formában tálaljuk.
Így alakult ez a Fraktálok esetbében is, ahol nem csak felfedeztük mikro- és makro szinten a különböző rendszerek és a természettudományok közötti összefüggéseket, de még szoftvert is fejlesztettünk Python nyelven a gyerekekkel!
Kezdjünk is bele, keressünk hasonlóságokat az alábbi fotókon! 

Pagodakarfiol

Hópehely

Páfrányok

Villámlás
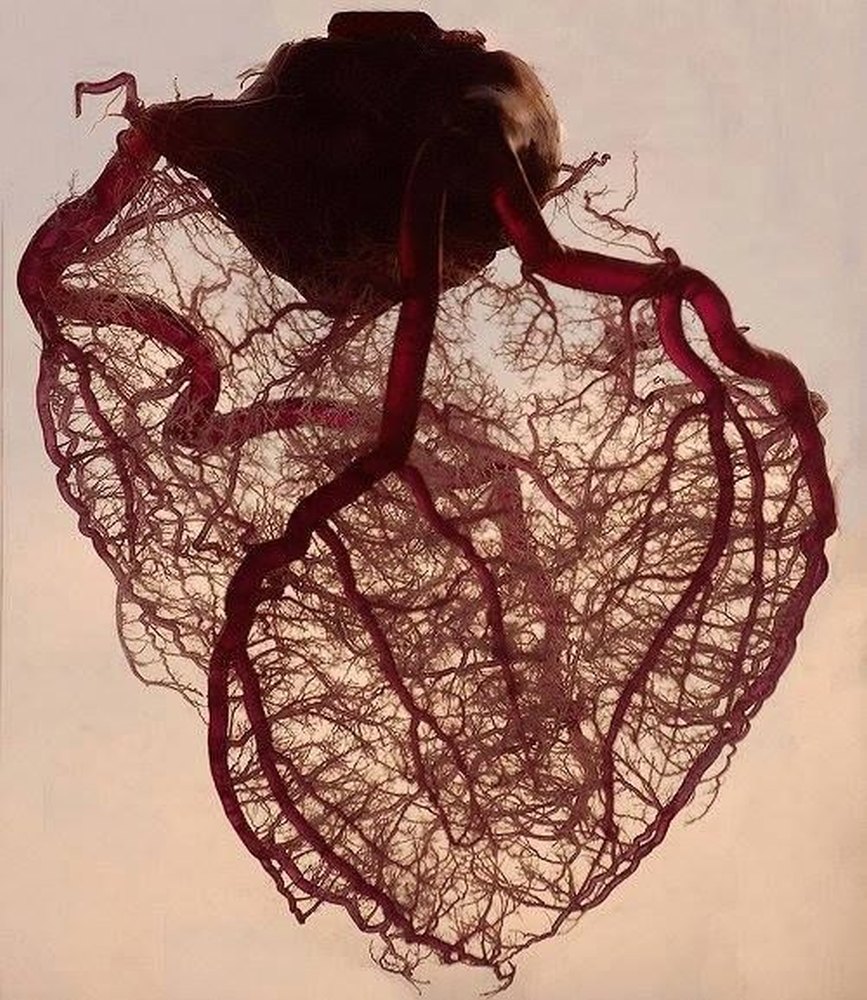
Az érrendszerünk
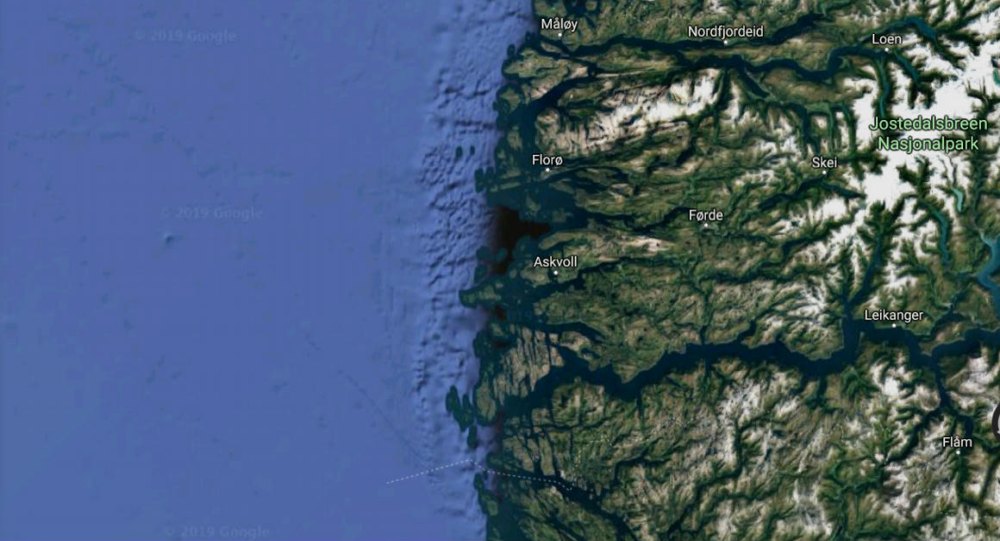
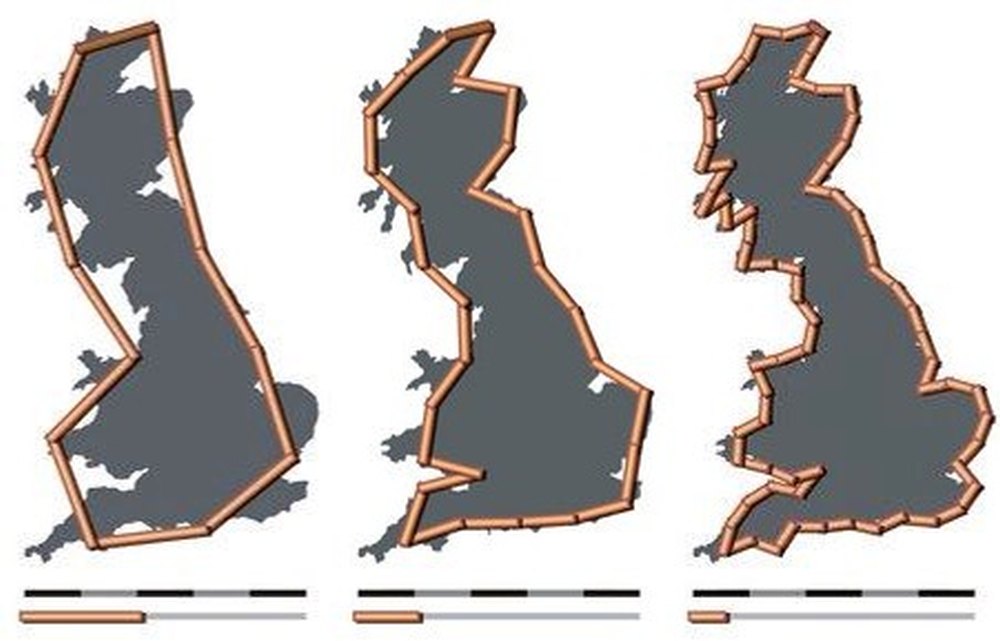
Norvégia partvonala

Namíbiai sivatag

Egyiptom

Dél-Afrika

Játékfejlesztés
A matematika tudománya közös lehet a fotókon?
Igen, mégpedig: A fraktálok

A fraktál geometria felfedezője Benoit Mandelbrot matematikus professzor volt (1975).
A fraktálok azok a “saját magukra hasonló” alakzatok, amelyeket egy matematikai formulával le lehet írni, vagy meg lehet alkotni, s valamely kisebb részük kinagyítva és elforgatva megegyezik az eredeti alakzattal.
A természet számtalan olyan objektummal / formával rendelkezik, amelyek többszöri nagyítás után is megtartják “eredeti alakjukat”.
Maximális részletességgel struktúráltak, maradnak még egy erős mikroszkópos nagyítással is.
A természetben az egyik leggyakrabban megtalálható fraktál a hópehely!
A kvantumfizika eredményei alapján a tudományban egy új típusú szerkezeti modell eshetősége van kialakulóban az Univerzum felépítésére vonatkozóan.
Ez az új modell fraktál jellegű.
Így kapcsolódik a kvantumfizika és a fraktál elmélet.
A fraktálok két csoportra oszthatók: Szabályos és véletlen fraktálok.
A természetben véletlen fraktálok találhatók meg! Ilyenek például a tengerek partvonalai, a folyóhálózatok, a jellemző tulajdonságuk az “önhasonlóság”.
Fraktálok hatékonysága a természetben

A fraktálok hiperhatékonyak, lehetővé teszik a növények számára, hogy maximalizálják a napfénynek való kitettséget, a hatékony fotoszintézist, a szív- és érrendszernek pedig, hogy a lehető leghatékonyabban szállítsa az oxigént a test minden részébe.
A fraktáldimenzió
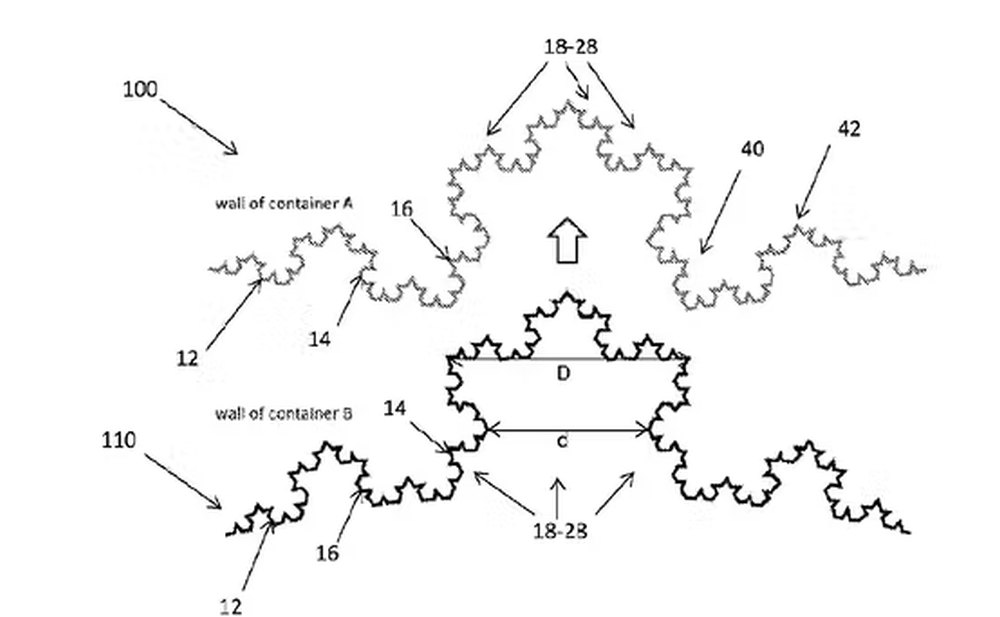
A fraktáldimenzió segítségével meghatározható, mennyire szabálytalan egy fraktál görbe.
Általában a vonalakat egydimenziósnak, a felületeket kétdimenziósnak, a testeket pedig háromdimenziósnak látjuk. Azonban egy nagyon tekervényes felület, mint pl. egy fa lombozata, vagy a tüdő belső felülete majdhogynem háromdimenziós lehet. Így a szabálytalanságra, hepehupásságra úgy tekinthetünk, mint a dimenzió növelésére: egy szabálytalan görbe dimenziója 1 és 2 között lesz, míg egy szabálytalan felületé 2 és 3 közé eseik.
Nézzünk egy bevezető példát, Python nyelven.
1 import turtle
2
3 def koch_fract(turtle, divis, size):
4 if divis == 0:
5 turtle.forward(size)
6 else:
7 for angle in [60, -120, 60, 0]:
8 koch_fract(turtle, divis - 1, size / 3)
9 turtle.left(angle)
10
11 divis = 7 # Hópehely bonyolultsága 7-11 között
12 size = 5000 # Hópehely mérete, 5000 - 100000 között
13
14 wn = turtle.Screen()
15 wn.setup(width=1000, height=500)
16 turtle.penup()
17 turtle.goto(-100, -150)
18 turtle.speed(100)
19 turtle.pendown()
20
21 for i in range(0, 30):
22 koch_fract(turtle, divis, size)
23 turtle.left(-120)




Folytatása következik... RoboKaland Csapat